1. 标准的神经网络

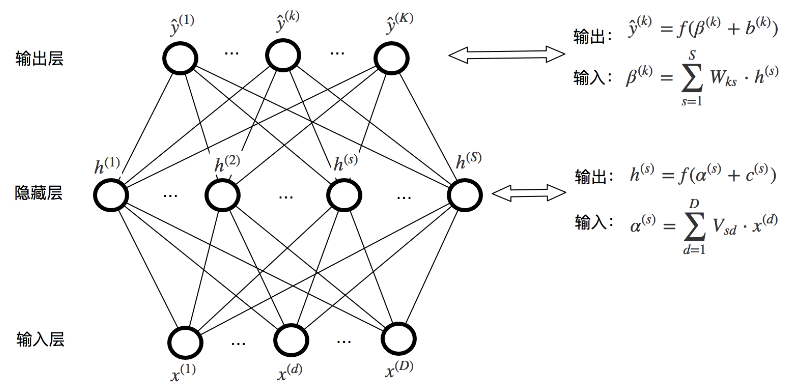
神经单元上的非线性映射函数 $f$ 是 $sigmoid$ 函数： $f(x)=\frac{1}{1+e^{-x}} \tag{1}$

$sigmoid$ 函数的导函数很有特点： $f^{'}(x)=f(x) \cdot \big( 1-f(x) \big) \tag{2}$

2. 推导过程

2.1 $Loss \, Function$

$Loss \, Function$: $\ell(\hat{y}, y)=\sum_{k=1}^K{ \big( \hat{y}^{(k)}-y^{(k)}} \big)^2 \tag{3}$
样本 $(x_i, y_i)$ 在模型上的均方误差为： $E_i=\frac{1}{2} \sum_{k=1}^K{ \big( \hat{y}_i^{(k)} -y_i^{(k)}\big)^2 } \tag{4}$ 注意：$y_i^{(k)}$中的$k$是指第$k$个输出单元，并不是指$k$次方

2.2 权值的梯度

误差从输出层反传到隐层，推导$\nabla W_{ks}$

$\begin{align*} \nabla W_{ks} & = \frac{\partial E_i}{\partial W_{ks}} \tag{5} \\ & = \frac{\partial E_i}{\partial \hat{y}_i^{(k)} } \cdot \frac{\partial \hat{y}_i^{(k)}}{ \partial \beta^{(k)}} \cdot \frac{\partial \beta^{(k)}}{\partial W_{ks}} \tag{6} \\ & = \underline {(\hat{y}_i^{(k)}-y_i^{(k)}) } \cdot \underline { \hat{y}_i^{(k)} \cdot (1-\hat{y}_i^k)} \cdot \underline {h^{(s)}} \tag{7} \end{align*}$

误差从隐层反传到输入层，推导$\nabla V_{sd}$

$\begin{align*} \nabla V_{sd} & = \frac{\partial E_i}{\partial V_{sd}} \tag{8} \\ & = \frac{\partial E_i}{\partial h^{(s)} } \cdot \frac{\partial h^{(s)}}{ \partial \alpha^{(s)}} \cdot \frac{\partial \alpha^{(s)}}{\partial V_{sd}} \tag{9} \\ & = \underline{ \sum_{k=1}^K{\frac{\partial E_i}{\partial \beta^{(k)}}\cdot \frac{\partial \beta^{(k)}}{\partial h^{(s)}}} } \cdot \underline{ h^{(s)} \cdot (1-h^{(s)}) } \cdot \underline{ x_i^{(d)} } \tag{10} \\ & = \underline{ \sum_{k=1}^K{\hat{y}_i^{(k)}(1-\hat{y}_i^{(k)})(\hat{y}_i^{(k)}-y_i^{(k)})W_{hk}} } \cdot \underline{ h^{(s)} (1-h^{(s)}) } \cdot \underline{ x_i^{(d)} } \tag{11} \end{align*}$

2.3 $bias$ 的梯度

输出层的$\nabla bias$ $\begin{align*} \nabla b^{(k)}&=\frac{\partial E_i}{\partial b^{(k)}}=\frac{\partial E_i}{\partial \hat{y}_i^{(k)}} \cdot \frac{\partial \hat{y}_i^{(k)}}{\partial b^{(k)}} \tag{12} \\ &=\underline{(\hat{y}_i^{(k)}-y_i^{(k)})} \cdot \underline{ \hat{y}_i^{(k)} \cdot (1-\hat{y}_i^{(k)}) } \tag{13} \end{align*}$
隐藏层的$\nabla bias$ $\begin{align*} \nabla c^{(s)}&= \frac{ \partial E_i }{ \partial c^{(s)} }= \frac{\partial E_i}{\partial h^{(s)}} \cdot \frac{\partial h^{(s)}}{ \partial c^{(s)}} \tag{14}\\ &= \underline{ \sum_{k=1}^K{\frac{\partial E_i}{\partial \beta^{(k)}}\cdot \frac{\partial \beta^{(k)}}{\partial h^{(s)}}} } \cdot \underline{ h^{(s)} \cdot (1-h^{(s)}) } \tag{15} \\ &= \underline{ \sum_{k=1}^K{\hat{y}_i^{(k)}(1-\hat{y}_i^{(k)})(\hat{y}_i^{(k)}-y_i^{(k)})W_{hk}} } \cdot \underline{ h^{(s)} \cdot (1-h^{(s)}) } \tag{16} \end{align*}$

3. 伪代码（用梯度下降法）

梯度下降算法训练神经网络:

4. SGD

为了解决梯度下降算法训练样本输入数据太大，学习速度太慢的问题，产生了一种新的算法叫做随机梯度下降算法 $Stochastic \;\; Gradient \,\, Descent$ 。随机选取的m个输入样本, ${ x_1, x_2,…, x_m }$ 称作 $mini-batch$ 。

$\nabla W \approx \frac{1}{m} \cdot \sum_{i=1}^m{ \nabla W_{x_i}} \tag{17}$

梯度下降和SGD的区别：

–标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的

–在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算

–标准梯度下降，由于使用真正的梯度，标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长

–如果标准误差曲面有多个局部极小值，随机梯度下降有时可能避免陷入这些局部极小值中

5. 向量化表示

为了实现神经网络方便，我们将其参数用矩阵或者向量表示。

5.1. 基础

黑体表示矢量或者矩阵，非黑体表示标量。假设当前层是 $l$，那么输入向量是：$\boldsymbol{z}^l$ $\boldsymbol{z}^l= \boldsymbol{W}^l \cdot \boldsymbol{a}^{l-1} + \boldsymbol{b}^l \tag{18}$

输出向量是：$ \boldsymbol{a}^l $ $\boldsymbol{a}^l= f(\boldsymbol{z}^l ) \tag{19}$

5.2. 推导

神经网络的损失在 $l$ 层上的传播误差向量化形式为：

$\boldsymbol{\delta}^l \stackrel{\rm def}{=} \frac{\partial J}{ \partial \boldsymbol{z}^l } = \begin{bmatrix} \delta_1^l \\ \delta_2^l \\ ...\\ \delta_n^l \end{bmatrix} = \begin{bmatrix} \frac{\partial J}{ \partial a_1^l } \dot \\ \frac{\partial a_1^l}{ \partial z_1^l } \\ \frac{\partial J}{ \partial a_2^l } \dot \\ \frac{\partial a_2^l}{ \partial z_2^l } \\ ...\\ \frac{\partial J}{ \partial a_n^l } \dot \\ \frac{\partial a_n^l}{ \partial z_n^l } \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial J}{ \partial a_1^l } \\ \frac{\partial J}{ \partial a_2^l } \\ ...\\ \frac{\partial J}{ \partial a_n^l } \\ \end{bmatrix} \otimes \begin{bmatrix} f'(z_1^l) \\ f'(z_2^l) \\ ...\\ f'(z_n^l) \\ \end{bmatrix} \\ = \frac{\partial J}{ \partial {\boldsymbol{a}}^l } \otimes \boldsymbol{f}'(\boldsymbol{z}^l) \tag{20}$

当 $l=L$ 时候， $\boldsymbol{\delta}^L = \frac{\partial J}{ \partial \boldsymbol{a}^L } \otimes \boldsymbol{f}'(\boldsymbol{z}^L) = (\boldsymbol{\hat{y}} - \boldsymbol{y}) \otimes \boldsymbol{f}'(\boldsymbol{z}^L) \tag{21}$

当 $l \not = L$ 时候， $\boldsymbol{\delta}^l = \frac{\partial J}{ \partial \boldsymbol{a}^l } \otimes \boldsymbol{f}'(\boldsymbol{z}^l) = \underline{ \frac{\partial J}{ \partial \boldsymbol{z}^{l+1}} \cdot \frac{\partial \boldsymbol{z}^{l+1}}{ \partial \boldsymbol{a}^l } } \otimes \boldsymbol{f}'(\boldsymbol{z}^L) = \underline{ \boldsymbol{\delta}^{l+1} \boldsymbol{W}^{l+1} } \otimes \boldsymbol{f}'(\boldsymbol{z}^l) \tag{22}$

对参数 $\boldsymbol{W} $ 的偏导数：

由于 $J$ 对 $w_{ij}^l$的导数为： $\frac{\partial J}{ \partial w_{ij}^l} = \frac{\partial J}{ \partial z_i^l} \cdot \frac{\partial z_i^l}{ \partial w_{ij}^l} = \delta_i^l \cdot a_j^{l-1} \tag{23}$

所以，总的损失对 $l$ 层的权重矩阵的偏导数为：

$\frac{\partial J}{ \partial \boldsymbol{W}^l } = \begin{bmatrix} \delta_1^l \cdot \boldsymbol{a}^{l-1} \\ \delta_2^l \cdot \boldsymbol{a}^{l-1} \\ ...\\ \delta_n^l \cdot \boldsymbol{a}^{l-1} \end{bmatrix} = \begin{bmatrix} \delta_1^l \\ \delta_2^l \\ ...\\ \delta_n^l \end{bmatrix} \cdot \left[a_1^l,a_2^l,...,a_m^l \right]= \boldsymbol{\delta}^l \cdot (\boldsymbol{a}^{l-1})^T \tag{24}$

对 $ \boldsymbol{b} $ 的偏导数：

由于 $J$ 对 $b_{i}^l$的导数为： $\frac{\partial J}{ \partial b_{i}^l} = \frac{\partial J}{ \partial z_i^l} \cdot \frac{\partial z_i^l}{ \partial b_{i}^l} = \delta_i^l \tag{25}$

所以，$J$ 对 $\boldsymbol{b}^l$的偏导数为： $\frac{\partial J}{ \partial \boldsymbol{b}^l} = \boldsymbol{\delta}^l \tag{26}$

Jarlonyan

神经网络