1. RNN的网络结构

1.1 论文中$RNN$的结构

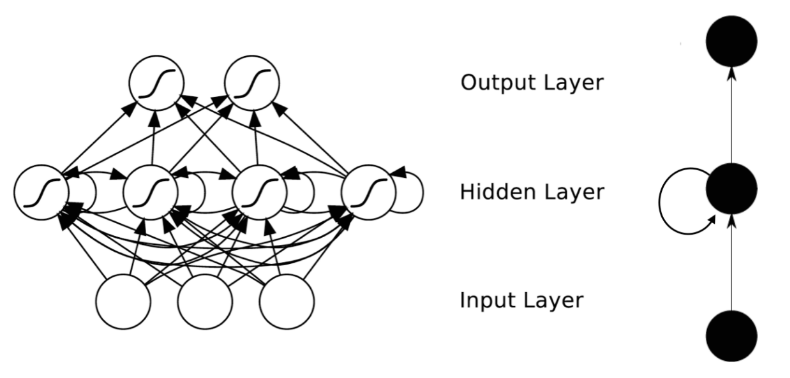
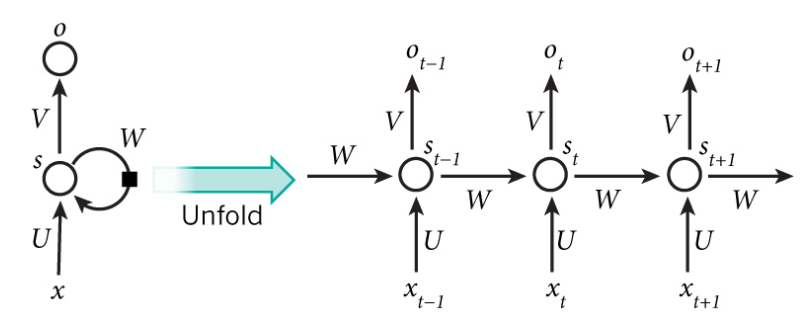
1.2 我的理解

     以前我们的样本是作为一个向量直接输入模型的。现在RNN中，一个样本拆分成若干个向量的序列，比如，句子拆分成词向量序列，$60 \times 80$的图像可以看成从上到下有60个向量序列。

     $RNN$ 的输入为$\big{ {x^0,x^1,…,x^t,x^{t+1},…} }$ ，而输出为$\big{ {y^0,y^1,…,y^t,y^{t+1},…} }$。这里的 $x^t$ 指的是 $t$ 时刻对应的那个单词的词向量。

     想象一下，如果将神经网络展开，会得到若干层的网络。比如，对一个包含10个单词的句子，那么展开的网络便是一个10级的神经网络，每一级代表一个单词。单词需要向量化 $(ont-hot, word2vec ,\, blabla…)$

权值是共享的，所以实际上只有第一幅图展示的网络结构。

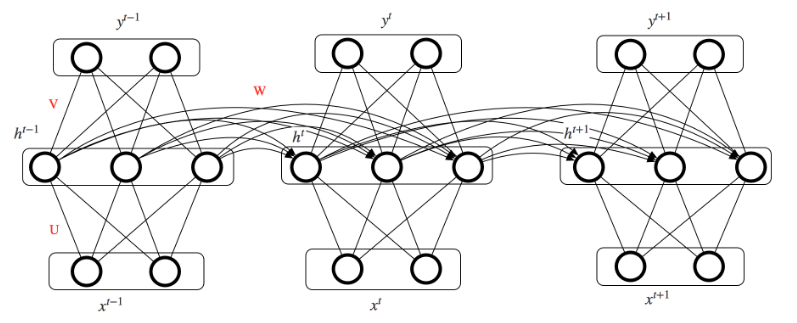
2. 模型推导

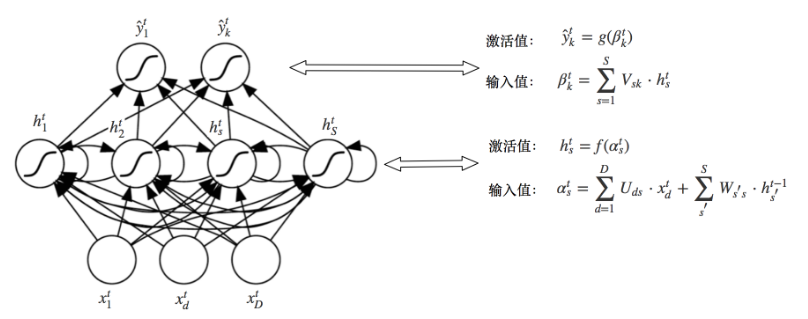
2.1 符号表示

     样本 $x$ 可以表示成若干个序列$\big{ {x^1, x^2, …, x^t,…,x^T} \big}$, 向量 $x^t$ 的维度都是$D$。注意：为了简单起见，我们没有$bias$，因为使用的是增广向量。      $x_d^t$ 表示 $t$ 时刻输入向量 $x^t$ 在第 $d$ 个维度的值。      $\alpha_s^t , \, h_s^t$ 分别表示隐藏层的输入值和激活值。      $\beta_k^t, \, \hat{y}k^t$ 分别表示输出层的输入值和激活值。      $U{ds}$ 表示输入层到隐藏层的权重      $V_{sk}$ 表示隐藏层到输出层的权重      $W_{ss^{‘}}$ 表示隐藏层到隐藏层的权重

2.2 前向传播

• $t$ 时刻的隐藏层

  隐藏层的第 $s$ 个节点，它的输入来源有两个，一个是 $t$ 时刻的输入，另一个是 $t-1$ 时刻的历史信息。 $t$ 时刻隐藏层第 $s$ 个单元的输入值： $\alpha_s^t=\sum_{d=1}^D{ U_{ds} \cdot x_d^t+ \sum_{s^{'}}^S{ W_{s^{'}s} \cdot h_{s^{'}}^{t-1} } } \tag{1}$

$t$ 时刻隐藏层第 $s$ 个单元的激活值： $h_s^t=f(\alpha_s^t) \tag{2}$

• $t$ 时刻的输出层

  $t$ 时刻输出层第 $k$ 个单元的输入值： $\beta_k^t=\sum_{s=1}^S{V_{sk} \cdot h_s^t} \tag{3}$

$t$ 时刻输出层第 $k$ 个单元的激活值： $\hat{y}_k^t=g(\beta_k^t) \tag{4}$

2.3 激活函数

• 激活函数:双曲正切函数 $tanh$ $f(x)=\frac{e^x-e^{-x}} { e^x+e^{-x} } \tag{5}$ 双曲正切函数的导函数： $f^{'}(x)=1-\big( f(x) \big)^2 \tag{6}$

• 激活函数 $Sigmoid$： $f(x)=\frac{1}{1+e^{-x}} \tag{7}$ 其导函数为： $f^{'}(x)=f(x) \cdot \big( { 1-f(x) } \big) \tag{8}$

2.4 $Loss \,\, Function$

• 可以是重构误差： $\begin{align*} \mathcal{L}(\hat{y}, y)&=\frac{1}{2} \cdot \sum_{t=1}^T{ { \big \lVert { \hat{y}^t-y^t } \big \rVert }^2 } \tag{9} \\ & =\frac{1}{2} \cdot \sum_{t=1}^T{ \sum_{k=1}^K{ \big( { \hat{y}_k^t-y_k^t } \big) }^2} \tag{10} \end{align*}$

• 也可以是交叉熵误差： $\mathcal{L}(\hat{y}, y)=-\sum_{t=1}^T{ \sum_{k=1}^K{ y_k^t \cdot \log{ \hat{y}_k^t } +(1-{y}_k^t) \cdot \log{(1-\hat{y}_k^t)} } } \tag{11}$

2.5 反向传播

    首先假设输出层单元的激活函数是 $g(x)$ ,隐藏层单元的激活函数是 $f(x)$ 。使用的 $Loss \,\, Function$ 是重构误差函数。

2.5.1 两个偏导数

• 误差对输出层输入值的偏导数 $\begin{align*} \delta_k^t & \stackrel{\rm def}{=} \frac{ \partial \mathcal{L} }{ \partial \beta_k^t } = \frac{\partial \mathcal{L}}{ \partial \hat{y}_k^t } \cdot \frac{\partial \hat{y}_k^t}{ \partial \beta_k^t } \tag{12} \\ & = \underline { \big( \hat{y}_k^t - y_k^t \big)} \cdot \underline { g^{'}(\beta_k^t)} \tag{13} \end{align*}$

• 误差对隐藏层输入值的偏导数 隐层的误差，一部分来自于输出层，另一部分来自于下一时刻的隐藏层。 $\begin{align*} \delta_s^t & \stackrel{\rm def}{=}\frac{ \partial \mathcal{L} }{ \partial \alpha_s^t } = \sum_{k=1}^K{ \frac{\partial \mathcal{L}}{ \partial \beta_k^t } \cdot \frac{\partial \beta_k^t}{ \partial h_s^t } \cdot \frac{\partial h_s^t}{ \partial \alpha_s^t } } \tag{14} \\ & = \sum_{k=1}^K{ \delta_k^t \cdot V_{sk} \cdot f^{'}(\alpha_s^t) } \tag{15} \end{align*}$

2.5.2 误差对 $U ,\, V ,\, W$ 的梯度

• 误差对 $V$ 的梯度 $\begin{align*} \nabla V_{sk} &=\frac{ \partial \mathcal{L} }{ \partial V_{sk} } = \sum_{t=1}^T{ \frac{\partial \mathcal{L}}{ \partial \beta_k^t } \cdot \frac{\partial \beta_k^t}{ \partial V_{sk} } } \tag{16} \\ & = \sum_{t=1}^T{ \delta_k^t \cdot h_s^t } \tag{17} \end{align*}$

• 误差对 $W$ 的梯度 $\begin{align*} \nabla W_{s^{'}s} &=\frac{ \partial \mathcal{L} }{ \partial W_{s^{'}s} } = \sum_{t=1}^T{ \frac{\partial \mathcal{L}}{ \partial \alpha_s^t } \cdot \frac{\partial \alpha_s^t}{ \partial W_{s^{'}s} } } \tag{18} \\ & = \sum_{t=1}^T{ \delta_s^t \cdot h_{s^{'}}^{t-1} } \tag{19} \end{align*}$

• 误差对 $U$ 的梯度 $\begin{align*} \nabla U_{ds} &=\frac{ \partial \mathcal{L} }{ \partial U_{ds} } = \sum_{t=1}^T{ \frac{\partial \mathcal{L}}{ \partial \alpha_s^t } \cdot \frac{\partial \alpha_s^t}{ \partial U_{ds} } } \tag{20} \\ & = \sum_{t=1}^T{ \delta_s^t \cdot x_d^t } \tag{21} \end{align*}$

3. 参考

[1] http://ir.hit.edu.cn/~jguo/docs/notes/bptt.pdf [2] http://blog.csdn.net/u011414416/article/details/46709965