1. 卷积神经网络

[TOC]

1. CNN基本结构

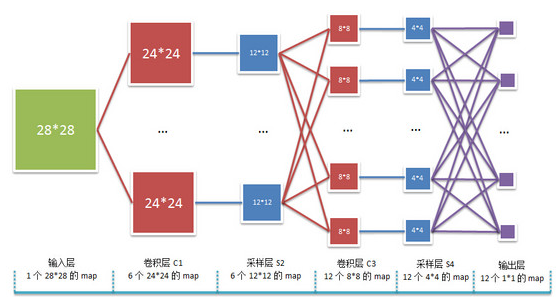
在CNN中输入是图像，权值W就是卷积模板，一般是卷积层和下采样层交替，最后是全连接的神经网络，也就是上述经典的人工神经网络。如下是一个简单的卷积神经网络示意图

2. 基础知识

2.1 局部感受野

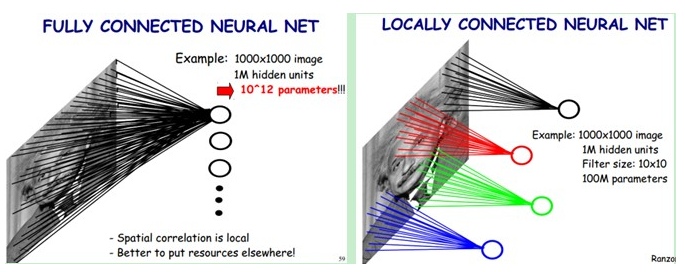
所谓的局部感受野，指的是隐藏层到输入层是局部连接，并不是全连接。普通的神经网络中，隐层节点会全连接到一个图像的每个像素点上，而在卷积神经网络中，每个隐层节点只连接到图像某个局部块上，从而大大减少需要训练的权值参数。举个栗子，依旧是1000×1000的图像，使用10×10的感受野，那么每个神经元只需要100个权值参数。

2.2 参数共享

即便是局部感受野，参数还是太多，那么需要参数共享（也叫权值共享）进一步减少参数。在上面的局部连接中，每个神经元都对应100个参数，一共1000000个神经元，如果这1000000个神经元的100个参数都是相等的，那么参数数目就变为100了。

怎么理解权值共享呢？我们可以这100个参数（也就是卷积操作）看成是提取特征的方式，该方式与位置无关。这其中隐含的原理则是：图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。

更直观一些，当从一个大尺寸图像中随机选取一小块，比如说 8x8 作为样本，并且从这个小块样本中学习到了一些特征，这时我们可以把从这个 8x8 样本中学习到的特征作为探测器，应用到这个图像的任意地方中去。特别是，我们可以用从 8x8 样本中所学习到的特征跟原本的大尺寸图像作卷积，从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。

2.3 卷积操作

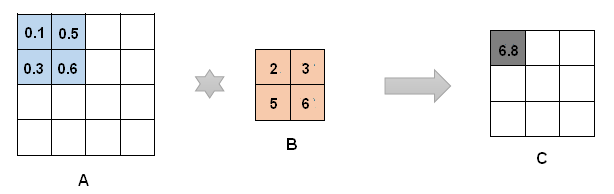
卷积运算表示为： $conv2(\boldsymbol{A}, \boldsymbol{B}) $ ，让B在A上滑动，对应位置上的元素的积之和构成结果C的一个元素。卷积运算有两种形式：窄卷积$ conv2(\boldsymbol{A}, \boldsymbol{B}, ‘valid’)$ 、宽卷积 $conv2(\boldsymbol{A}, \boldsymbol{B}, ‘full’)$。一般的是窄卷积，如果矩阵A的上下左右预先添加一些零向量，那么就是宽卷积。卷积操作得到的C就是特征图，也叫 $feature \; map$ 。在上面的CNN的构造图中，每一层是由多个$feature \; map$ 构成的，每个$feature \; map$ 中含有很多神经元。

3. 前向传播

3.1. 卷积层

假设当前层是 $l$，那么输入是：$\boldsymbol{U}_i^l$ $\boldsymbol{U}_i^l=\sum_{j=1}^{N_{l-1}}{ conv2(\boldsymbol{A}_j^{l-1}, \boldsymbol{K}_{ij}^l) + b_{ij}^l} \tag{1}$

输出： $ \boldsymbol{A}_i^l $ $\boldsymbol{A}_i^l =f(\boldsymbol{U}_i^l) \tag{2}$ （说明：英文字母的黑体大写表示矩阵，英文字母的非黑体小写表示标量。）

3.2. 池化层

输入：$\boldsymbol{U}_i^l$ $\boldsymbol{U}_i^l= \beta_i^l \cdot down(\boldsymbol{A}_i^{l-1})+b_i^l \tag{3}$

输出： $ \boldsymbol{A}_i^l $ $\boldsymbol{A}_i^l =f(\boldsymbol{U}_i^l) \tag{4}$

4. 误差反向传播

4.1. 全连接层

全连接层的反向传播求导和BP神经网络是一样的。 $\frac{\partial J}{ \partial \boldsymbol{W}^l} =\boldsymbol{\delta}^l ( \boldsymbol{x}^{l-1})^T \tag{5}$

$\frac{\partial J}{ \partial \boldsymbol{b}^l} =\boldsymbol{\delta}^l \tag{6}$

4.2. 卷积层

误差在卷积层的敏感性： $\begin{align*} \boldsymbol{\delta}_i^l & \stackrel{\rm def}{=} \tag{7} \frac{\partial J}{ \partial \boldsymbol{U}_i^l } \\ & = \frac{\partial J}{ \partial \boldsymbol{A}_i^l } \otimes \frac{\partial \boldsymbol{A}_i^l}{ \partial \boldsymbol{U}_i^l } \tag{8} \\ & = \frac{\partial J}{ \partial \boldsymbol{U}_i^{l+1} } \cdot \frac{\partial \boldsymbol{U}_i^{l+1}}{ \partial \boldsymbol{A}_i^l } \otimes f'(\boldsymbol{U}_i^l) \tag{9} \\ & = up(\boldsymbol{\delta}_i^{l+1}) \cdot \beta_i^{l+1} \otimes f'(\boldsymbol{U}_i^l) \tag{10} \\ & = \beta_i^{l+1} \cdot up(\boldsymbol{\delta}_i^{l+1}) \otimes f'(\boldsymbol{U}_i^l) \tag{11} \end{align*}$

在上面公式中，本来 $\frac{\partial J}{ \partial \boldsymbol{U}_i^{l+1} }$ 得到的是 $ \boldsymbol{\delta}_i^{l+1} $ ，但是 $ \boldsymbol{\delta}_i^{l+1} $ 和当前的卷积层的feature map的宽度和高度并不相同，这是因为之前采用了下采样操作，所以，为了保证能够和后面的矩阵相乘，需要对$ \boldsymbol{\delta}_i^{l+1} $ 做一个上采样操作。此外， $\beta_i^{l+1}$ 是一个标量，自然可以提到前面去。 $\otimes$ 运算是指两个矩阵的对应位置上的元素进行相乘，得到一个新的矩阵，它并不是矩阵的乘法运算。 $\boldsymbol{\delta}_i^l$ 是二维的。

误差对卷积层的参数求偏导数： $\frac{\partial J}{\partial b_{i}^l} = \sum_{s,t}{ (\boldsymbol{\delta}_i^l)_{st} } \tag{12}$

$\begin{align*} \frac{\partial J}{\partial \boldsymbol{K}_{ij}^l} & = \sum_{s,t}{ (\boldsymbol{\delta}_i^l)_{st} (P_j^{l-1})_{st}} \tag{13} \\ &=rot180( conv2(A_j^{l-1}, rot180 \big( \boldsymbol {\delta}_i^l)) \big) \tag{14} \end{align*}$

$(P_j^{l-1}){st}$ 是 $(\boldsymbol{\delta}_i^l){st}$ 所连接的 $l-1$ 层中 $\boldsymbol{A}_j^{l-1}$ 中相关的元素构成的矩阵。公式(14)是文献[2]中提到的。

4.3. 池化层

误差在池化层的敏感性： $\begin{align*} \boldsymbol{\delta}_i^l & \stackrel{\rm def}{=} \tag{15} \frac{\partial J}{ \partial \boldsymbol{U}_i^l } \\ & = \frac{\partial J}{ \partial \boldsymbol{A}_i^l } \otimes \frac{\partial \boldsymbol{A}_i^l}{ \partial \boldsymbol{U}_i^l } \tag{16} \\ & = \frac{\partial J}{ \partial \boldsymbol{U}_i^{l+1} } \cdot \frac{\partial \boldsymbol{U}_i^{l+1}}{ \partial \boldsymbol{A}_i^l } \otimes f'(\boldsymbol{U}_i^l) \tag{17} \\ & = \sum_{j=1}^{N_l}{f'(\boldsymbol{U}_i^l) \otimes conv2( \boldsymbol{\delta}_i^{l+1}, \boldsymbol{K}_{ij}^{l+1}) } \tag{18} \end{align*}$

误差对池化层的参数求偏导数： $\frac{\partial J}{\partial b_{i}^l} = \sum_{s,t}{ (\boldsymbol{\delta}_i^l)_{st} } \tag{19}$

$\frac{\partial J}{\partial \beta_i^l} = \sum_{s,t}{ (\boldsymbol{\delta}_i^l \otimes d_i^{l-1} )_{st}} \tag{20}$

其中，$d_i^{l-1}=down(A_i^{l-1})$ 。